おおまかには

$C_{\le k}$-free 2-マッチング問題とはグラフ上の最適化問題で，「2-マッチング」という効率的に扱える対象に「$C_{\le k}$-free」というハミルトン閉路に近づく制約を付けたものを扱う問題です． グラフのハミルトン性の解析や，巡回セールスマン問題に対する近似アルゴリズム設計への応用などを主な動機として研究されています．

正確な定義は

• 2-マッチング
  グラフ $G$ を平行辺や自己閉路をもたない単純無向グラフとします． 2-マッチングとは，各頂点に接続する辺が 2 本以下である辺部分集合と定義されます． 各頂点に接続する辺が丁度 2 本であるときは，特に 2-因子 とよばれます．

  例えば，下図 (a) における赤色の辺集合は，中央の頂点に 3 本の辺が接続しているので 2-マッチングではありません． 一方，下図 (b)，(c) における赤色の辺集合はいずれも 2-マッチングで，特に (c) は 2-因子となります．

  

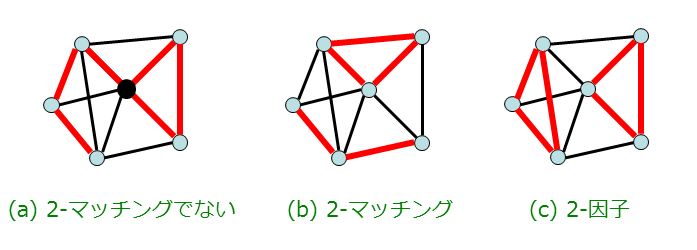
  2-マッチング問題とは，与えられた単純無向グラフ $G$ において辺数最大の 2-マッチングを求める問題です． 例えば，2-因子が見つかった場合はそれが最適解となります． あるいは，2-因子が見つからない場合でも，ある 2-マッチングについてその辺数が最大であることを何らかの方法で証明できれば，問題が正しく解けたことになります． 2-マッチング問題は，(例えばマッチング問題に帰着することによって) 高速に解けることが知られています．

• $C_{\le k}$-free 2-マッチング
  上図 (b)，(c) の例からもわかるとおり，2-マッチングはパスと閉路の点素な集まり，2-因子は閉路の点素な集まりで各頂点を一度ずつ通るものとなります． 「$C_{\le k}$-free」とは，この閉路の長さ対する制約です． 2-マッチング (2-因子) $M$ が長さ $k$ 以下の閉路を含まないとき，$M$ は $C_{\le k}$-free 2-マッチング ($C_{\le k}$-free 2-因子) であると定義されます．

  したがって，$k$ の値が大きいほど制約は厳しくなります． 下図の四つの辺集合はいずれも辺数が 16 の 2-因子ですが，含まれる閉路の長さによってどの $k$ の値まで $C_{\le k}$-free の制約をみたすかが異なります．

  

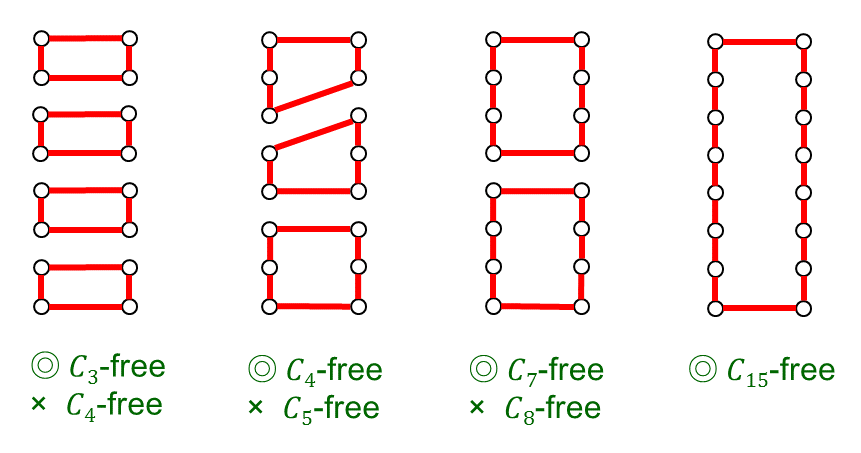
  $C_{\le k}$-free 2-マッチング問題は，単純無向グラフ $G=(V,E)$ と正整数 $k$ に対して辺数最大の $C_{\le k}$-free 2-マッチングを求める問題となります．

ハミルトン閉路と $C_{\le k}$-free 2-因子の関係

ハミルトン閉路とは，全頂点を一度ずつ通る一つの閉路と定義されます． 例えば上図右端の $C_{\le 15}$-free 2-因子は，頂点数 16 のグラフにおけるハミルトン閉路です． 与えられたグラフにおいてハミルトン閉路を見つける問題 (ハミルトン閉路問題) は，離散数学・グラフ理論における基本的な問題で，高速な解法は知られていません．

ハミルトン閉路は，特殊な 2-因子ととらえることができます． ハミルトン閉路を長さが頂点数 $n$ の閉路からなる 2-因子と言い換えると，$C_{\le k}$-free 2-因子との関連が見えてきます． すなわち，ハミルトン閉路は $k \le n-1$ の範囲で $C_{\le k}$-free の性質をみたす 2-因子です．

さらに，$k \ge \lfloor n/2 \rfloor$ のとき，$C_{\le k}$-free 2-因子はハミルトン閉路であることがすぐにわかります (以下，簡単のため $\lfloor \cdot \rfloor$ 記号を省略します)． $k$ の値を $n/2$ からさらに小さくしていくと，より多くの 2-因子が $C_{\le k}$-free となっていきます (上図の例を右から左にたどることに対応します)． 最後に，$k=2$ のときは，$C_{\le 2}$-free 2-因子は 2-因子に一致します．

つまり， $k$ の値を $ n/2 $ から小さくしていくと，ハミルトン閉路から 2-因子に向かって緩和していくことになります． 2-因子問題は高速で解けるためハミルトン閉路問題を解く足がかりとして 2-因子を用いる方法は広く考えられてきましたが，$k$ の値を調整してハミルトン閉路により近い 2-因子からアプローチするというのが $C_{\le k}$-free 2-マッチング問題を考える主な動機です．

応用例

$C_{\le k}$-free 2-因子の具体的な応用例を一つ見てみましょう． 最小全域オイラー部分グラフ問題とよばれる，やはりグラフ上の最適化問題があります． この問題は，与えられた単純無向グラフ $G$ において，任意の頂点から始めて全頂点を一度以上通って元の頂点へ戻ってくる，最も通る辺数の少ないたどり方を求める問題です． ここでは，同じ辺を 2 度以上通ってもよいこととします． 例えば，下図 (ア)，(イ) の赤の辺集合はそれぞれ，同じ単純無向グラフにおける最小全域オイラー部分グラフ問題の解です．

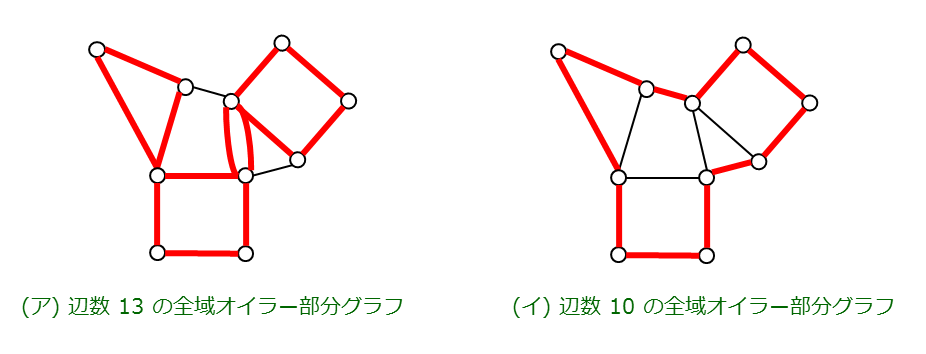
全頂点を通って元の頂点まで戻ってくるという点はハミルトン閉路と同じですが，各頂点・辺を二度以上通っても良いという点が異なります． また，もしグラフにハミルトン閉路が存在した場合は最適解となります． したがって，最小全域オイラー部分グラフ問題はハミルトン閉路問題を含む，やはり難しい問題です． さらには，最小全域オイラー部分グラフ問題はグラフ的巡回セールスマン問題とよばれる巡回セールスマン問題のクラスと一致することが知られています．

さて，$C_{\le k}$-free 2-因子を用いると，最小全域オイラー部分グラフ問題の近似アルゴリズムが設計できます． 近似アルゴリズムとは，最適解ではなくても，ある程度「良い」(この問題の場合は辺数の少ない) 解を見つけるアルゴリズムです．

$G$ における $C_{\le k}$-free 2-因子 $M$ が一つ見つかったとしましょう． すると，

1. $M$ の閉路をすべて縮約，
2. 縮約したグラフにおける最小木 $T$ をとり，$T$ の枝を二重にする ($2T$ と書くこととします)，
3. $G$ において，$M$ と $2T$ の和 $F$ を出力

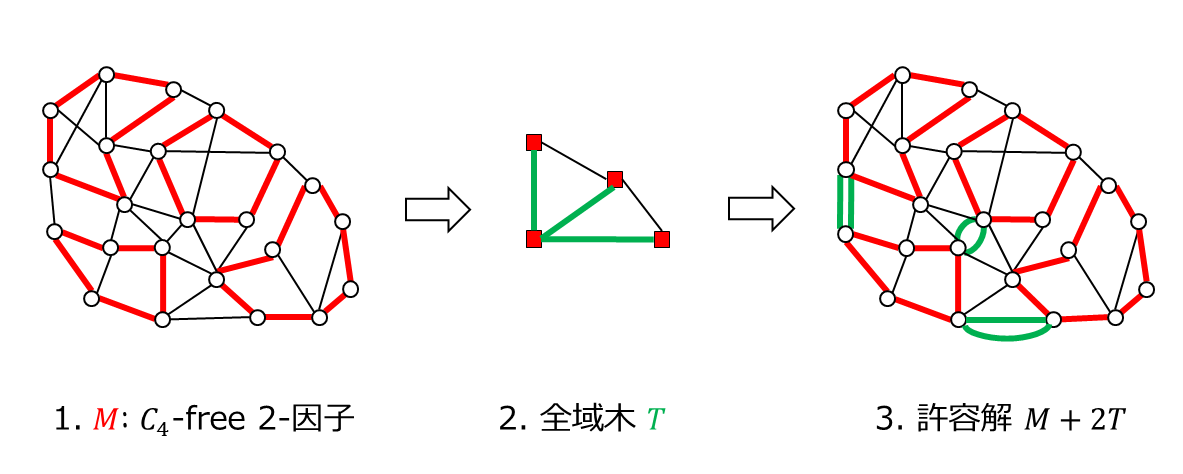
このとき，$M$ が $C_{\le k}$-free であるという性質から $F$ の辺数を見積もることができます． $M$ に含まれる閉路の長さが $k+1$ 以上であることから $|T| \le \frac{n}{k+1} - 1$ となり，$|F| = |M| + 2|T| \le n + 2 (\frac{n}{k+1} -1)$ が得られます． 最適解の辺数は $n$ 以上なので，$F$ の辺数は最適解の高々 $\left(1+\frac{2}{k+1} - \frac{2}{n}\right)$ 倍となります．

計算複雑度 (先行研究)

それでは，$C_{\le k}$-free 2-マッチング問題を解くことはできるのでしょうか？ 前述のとおり $k=2$ の場合は古典的な 2-マッチング問題となり，高速に解くことができます (クラス P に属する問題といいます)． また，$k \ge n/2 $ の場合は，ハミルトン閉路問題を含む，難しい問題となります (NP 困難な問題といいます)．

それ以外の $k$ の値について知られている結果は下表のとおりです． 「重み付き」とは，辺重みベクトル $w \in \mathbf{R}_{\ge0}$ が与えられて，$\sum_{e \in M} w(e)$ 最大の $C_{\le k}$-free 2-マッチング $M$ を求めるという問題です． こちらは特に，巡回セールスマン問題に関連しています．

一般グラフにおいては Hartvigsen (1984) による $C_{\le 3}$-free 2-マッチングアルゴリズム以降目立った進展はありませんが，２部グラフにおいては 2000 年前後以降に活発に研究がなされています． また，subcubic graph (= 各頂点に接続する辺の数が 3 以下のグラフ) においても多くの成果があります． 問題の記述はとてもシンプルですが未だに解決されていないケースも残されており，離散数学らしい取り組みがいのある問題だと思います．

一般グラフ 重みなし 重み付き $k \ge 5$ NP 困難 [Papadimitriou 1978] NP 困難 [Papadimitriou 1978] $k = 4$ 未解決 NP 困難 [Vornberger 1980] $k = 3$ P [Hartvigsen 1984] 未解決 $k = 2$ P P

２部グラフ 重みなし 重み付き $k \ge n/2 $ NP 困難 NP 困難 $k \ge 6$ NP 困難 [Geelen 1999] NP 困難 [Geelen 1999] $k = 4$ P [Pap 2006, Hartvigsen 2007] NP 困難 [Király 2003] $k = 2$ P P

私の研究 (少しテクニカルな話)

1. ２部グラフにおける重み付き $C_{\le 4}$-free 2-マッチングの組合せ的アルゴリズム
   上記のとおり，重み付き $C_{\le 4}$-free 2-マッチングは２部グラフにおいても NP 困難ですが， 重みが「ある性質 (★)」をみたす場合は線形計画問題を解くことで整数解が得られることが知られていました． 本研究では性質 (★) の問題設定に対し，線形計画問題の一般解法を用いずに問題を解く組合せ的主双対アルゴリズムを設計しました．
   
   • K. Takazawa: A weighted $K_{t,t}$-free $t$-factor algorithm for bipartite graphs, Mathematics of Operations Research, 34 (2009), pp. 351-362.

2. 一般グラフにおける $C_{\le 4}$-free 2-マッチングの離散凸性の証明
   上表のとおり，一般グラフにおける $C_{\le 4}$-free 2-マッチング問題の計算複雑度は未解決です． Cunningham (2002) は，$C_{\le 4}$-free 2-マッチングの次数列全体がジャンプシステムとよばれる離散凸構造を成すと予想し， 本研究ではこの Cunningham の予想が正しいことを証明しました． ジャンプシステムは効率的に扱うことのできる組合せ最適化問題の多くに現れる構造で，この結果により $C_{\le 4}$-free 2-マッチング問題はクラス P に属することが予想されます．
   さらに，２部グラフにおける重み付き $C_{\le 4}$-free 2-マッチングがジャンプシステム上のＭ凸関数とよばれる離散凸関数を導出する必要十分条件が，辺重みの性質 (★) であることを証明しました． ジャンプシステム上のＭ凸関数もやはり効率的に扱うことのできる重み付き組合せ最適化問題の多くに現れる関数で，研究 1 で述べた計算複雑度と対応がとれていることがわかります．
   
   • Y. Kobayashi, J. Szabó and K. Takazawa: A proof of Cunningham's conjecture on restricted subgraphs and jump systems, Journal of Combinatorial Theory, Series B, 102 (2012), pp. 948-966.

3. ２部グラフにおける $C_{\le 4}$-free 2-マッチングの分解定理
   ２部グラフにおける $C_{\le k}$-free 2-マッチングに対して，Dulmage-Mendelsohn 分解や Edmonds-Gallai 分解に対応する分解定理を証明しました． Hartvigsen (2006) のアルゴリズムから求まる二つの最小化元が正準的であることや，その二つの正準的最小化元を用いた最大 $C_{\le 4}$-free 2-マッチングの特徴付けが得られました．
   
   • K. Takazawa: Decomposition theorems for square-free 2-matchings in bipartite graphs, Discrete Applied Mathematics, 233 (2017), pp. 215-223.

4. 正則２部グラフにおける $C_{\le 4}$-free 2-因子と近似アルゴリズム
   各頂点に接続する辺数がすべて等しい２部グラフ (正則２部グラフ) においては $C_{\le 4}$-free 2-因子が必ず存在することを証明しました． これにより，上記の方法を用いて最小全域オイラー部分グラフ問題に対する 4/3-近似アルゴリズムを得ました． また，やはりハミルトン閉路問題を含む NP-困難な問題である最小２辺連結全域部分グラフ問題に対する 4/3-近似アルゴリズムも得られました．
   本論文ではさらに，各頂点に接続する辺数が３であり任意の２辺を削除しても連結である正則２部グラフにおいて，最小２辺連結全域部分グラフ問題に対する 7/6-近似アルゴリズムを設計しました．
   
   • K. Takazawa: A 7/6-approximation algorithm for the minimum 2-edge connected subgraph problem in bipartite cubic graphs, Information Processing Letters, 116 (2016), pp. 550-553.
   • K. Takazawa: Approximation algorithms for the minimum 2-edge connected spanning subgraph problem and the graph-TSP in regular bipartite graphs via restricted 2-factors, RIMS Preprint, RIMS-1826, Kyoto University, 2015.

5. $C_{\le k}$-free 2-マッチングの一般化
   $C_{\le k}$-free 2-マッチングの一般化として，$\mathcal{U}$-実行可能 2-マッチングを提案しました． 頂点の部分集合族 $\mathcal{U}\subseteq 2^V$ に対し $\mathcal{U}$-実行可能 2-マッチングとは，任意の $U \in \mathcal{U}$ の中での 2-因子を含まない 2-マッチングと定義されます． 巡回セールスマン問題において，$\mathcal{U}\subseteq 2^V$ に対してのみ部分巡回路除去制約を課した 2-マッチングと理解することもできます． したがって，$\mathcal{U}$-実行可能 2-マッチング問題は難しい問題ということになりますが，本論文では２部グラフにおいて「任意の $U \in \mathcal{U}$ が Hamilton-laceable なグラフを誘導する」という仮定のもとでの効率的なアルゴリズムを設計しました． この仮定は $C_{\le 4}$-free 2-マッチング問題の一般化であり，他には例えば「任意の $C_6$ が 2 本以上のコードをもつ場合の $C_{\le 6}$-free 2-マッチング問題」などが含まれます． つまり，$k \ge 5$ において効率的に解ける $C_{\le k}$-free 2-マッチング問題のクラスを初めて与えたことになります．
   
   • K. Takazawa: Finding a maximum 2-matching excluding prescribed cycles in bipartite graphs, Discrete Optimization, 26 (2017), pp. 26-40.

6. さらなる一般化
   $\mathcal{U}$-実行可能 2-マッチングのさらなる一般化である $\mathcal{U}$-実行可能 $t$-マッチングの枠組を提案しました． 本研究は上記の研究 5. を整数 2 から一般の整数 $t$ に単に一般化しただけではなく，
   1. 一般グラフにおけるマッチング問題，
   2. 一般グラフにおける $C_3$ を禁止する 2-マッチング (ただし，２重辺を含んでよいという点で上記の $C_{\leq 3}$-free 2-マッチングとは異なります)，
   3. ２部グラフにおける $C_{\leq 4}$-free 2-マッチング
   など，マッチング問題の様々な一般化が含まれます． 本研究ではさらに，ある条件をみたす２部グラフにおいて $\mathcal{U}$-実行可能 $t$-マッチングの最大最小定理，双対整数性をもつ線形計画表現，および組合せ的アルゴリズムを与えました． 上記の問題 1-3 はいずれも この条件をみたす $\mathcal{U}$-実行可能 $t$-マッチング問題で記述されます． 特に，一般グラフにおける問題 1, 2 が２部グラフにおける $\mathcal{U}$-実行可能 $t$-マッチング問題で記述されることが特徴的です． 上記のマッチングの一般化それぞれに対してはマッチング理論における主要な結果の拡張が為されていましたが，これらの相互の関係は見出されておりませんでした． 本研究では，$\mathcal{U}$-実行可能 $t$-マッチングの組合せ的アルゴリズムの設計を通じて，上記のマッチング問題の様々な一般化を包括する理論を構築し，統一的な理解を与えました．
   
   • K. Takazawa: Excluded $t$-factors in bipartite graphs: A unified framework for nonbipartite matchings, restricted 2-matchings, and matroids, SIAM Journal on Discrete Mathematics, 36 (2022), pp. 702-727.